高考最后3个月数学成绩还能怎样提升?这几个解题技巧要知道
从现在到离2024年高考仅剩不到90天的时间,想要在剩下的备考时间里取得进步,需要采取适当的策略。以下策略需要在平时的练习中进行巩固并且加以掌握。新高考改革的命题方向就是:“解放思想,避免惯性思维”。
在解题过程中,重视培养解题速度和准确率。正如前文所述,当面对选择题和填空题时,尽量运用特殊方法。
①特殊值法。需要特别强调的是,并非所有数值都能成为特殊值。举例来说,当给定一个抽象函数的解析式以及其他相关条件时,我们可以列举出符合条件的具体函数解析式,作为特殊值的一种形式。这就是所谓的“万法归宗”。
例如:若在选择、填空题中给出抽象函数的表达式f(x+y)=f(x)f’(y)+f’(x)f(y),f(2)=-f(1)!=0。求一些f(1/2)或其他的函数值。为了快速解决该问题,我们可以为抽象函数找到一个特殊的解析式sin(A+B)=sinAcosB+sinBsinA。但是因为存在f(2)和f(-1)不能等于0,那么是不能直接利用sin(A+B),既然我们有了方向,可以设f(x)=Asinwx,将2和-1带入求出A和w,从而求解出具体的解析式。
此外还有很多基本函数的形如f(x+y)=f(x)+f(y)指数形式的一般式。大家在平时练习中多做总结。
②数形结合法。只要图形做的精确,甚至可以使用尺子、量角器直接量出相关量,避免大量计算,并保证正确率。(标准的网格线最好,例如T9 B卷关于北斗七星的题目)。这里再拿出该图说明一下最后一个选项。
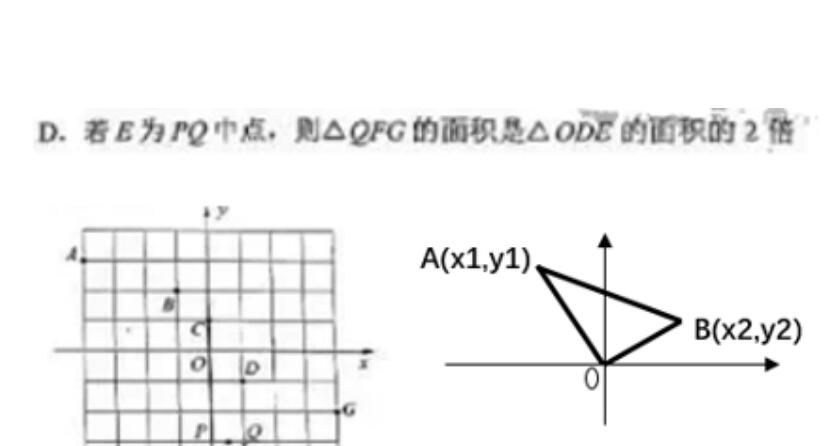
要比较的是三角形的面积,我们先看右图,S=|x1*y2-x2*y1|/2,自己推一下很简单。
③代入法。将给出的选项带入题设条件是否满足题意。Ex:九省联考B卷的第十道多选题(排列组合问题)

【解析】
概率统计和排列组合模块的知识点相对独立,即使在联立考察时,也通常与点坐标关系(如圆锥曲线)或数列部分有关。然而,由于这些知识点的独立性,以及考试要求的思维逻辑要求较高(常常导致考虑不周全而失分),它们与未来人工智能的神经网络,如当前非常流行的“扩散模型”,以及一些芯片计算的运算算法密切相关。因此,这些内容也成为未来高考的重点和难点。
此外,该部分的涉及到的数学符号特别多,T9 A卷还给出了很多数学符号的新定义。所以学习过程中,需要深入理解每个概念和数学符号,并做一些经典的题目。训练自己的思维逻辑。争取拿到这部分分值(很有诱惑的,不出意外,24年高考数学一般会有17分的综合大题)。

④转化法。题目要求的是A问题,通过逻辑分析A问题的本质就是B问题,转化成自己熟悉或复习阶段做过大量练习的题目进行求解。转化法相对较为复杂,这里涉及到了分析,这也是大家比较头痛的问题。下面举个简单的例子予以说明。
例1:若0<A<π/2,则f(A)=1/sinA^2+16/cosA^2,求f(A)最大值______。
【解析】表面上看这道题是关于三角函数的题目,实际上是考察的不等式。大家看看使用哪个公式呢?(答案是权方和不等式)。这类题有非常强的迷惑性,但是从问题出发还是可以窥见一二的。求最值的方法有哪些呢?不等式、函数导数等等。
例2:点A(-2,0),B(-0.5,0),C(0,1),若动点P满足|PA|=2|PB|,且向量AP、AB、AC 满足AP=λAB+μAC,则λ+3μ的最大值______。
【解析】
这是一个涉及几何(动点问题)、向量等知识点的题目,需要求解参数代数式的值。我们需要计算λ+3μ。为了做到这一点,我们必须利用给定的条件进行转换。首先,我们来考虑动点P的轨迹是什么。如果我们之前对所学内容有充分的复习和总结,那么很容易就能看出来,P的轨迹是一个单位圆。这个结论也可以通过自己推导得出(类似于阿氏圆的推导)。既然是单位圆,利用三角代换,将向量将AP、AB、AC表示成点的形式,λ、μ转化成坐标点的关系。最后将λ、μ分别表示出来,进而表示成λ+3μ,即可算出最大值。
- 热门课程
- 热门资讯
- 热门资料
- 热门福利
-
 黄河小班课人数多吗?教学效果怎么样?黄河小班课之前就有家长和学生想要了解过,今天为了满足大家的要求,小编就来好好给大家解答一下关于黄河小班课的一些内容,让大家能够更加方便地做出选择。 一、黄河小班课人数多吗? 黄河小班课的人数控制得挺讲究,既不是那种三五个人的微型小组,也不会像其他学校那样挤着四五十个人,一个班大概在6到15人
黄河小班课人数多吗?教学效果怎么样?黄河小班课之前就有家长和学生想要了解过,今天为了满足大家的要求,小编就来好好给大家解答一下关于黄河小班课的一些内容,让大家能够更加方便地做出选择。 一、黄河小班课人数多吗? 黄河小班课的人数控制得挺讲究,既不是那种三五个人的微型小组,也不会像其他学校那样挤着四五十个人,一个班大概在6到15人 -
 “白驹过隙”怎么读?到底有什么含义?“白驹过隙” 是形容时光的经典表达,可你真能笃定 “驹” 字读 “jū” 而非 “jú”?而且 “白驹” 为何是 “白色的小马”,“过隙” 又特指什么缝隙? 一、“白驹过隙”怎么读? “白驹过隙”的正确读音是bái jū guò xì,“白驹”指白色的骏马,常被引申为太阳的光芒或飞速流逝的时
“白驹过隙”怎么读?到底有什么含义?“白驹过隙” 是形容时光的经典表达,可你真能笃定 “驹” 字读 “jū” 而非 “jú”?而且 “白驹” 为何是 “白色的小马”,“过隙” 又特指什么缝隙? 一、“白驹过隙”怎么读? “白驹过隙”的正确读音是bái jū guò xì,“白驹”指白色的骏马,常被引申为太阳的光芒或飞速流逝的时 -
 博大单招在文化课提升方面优势如何?补习效果好吗?单招相信第一次接触的家长和同学们有很多问题都不了解,很多家长为了让孩子更好地学习就去选择一个合适的单招补习,那么博大单招在这方面的优势到底怎么样?能不能帮助孩子更好地提升呢?今天我们就来一起好好了解一下。 一、博大单招在文化课提升方面优势如何? 博大单招在文化课提升这方面那真的是研究得透透的
博大单招在文化课提升方面优势如何?补习效果好吗?单招相信第一次接触的家长和同学们有很多问题都不了解,很多家长为了让孩子更好地学习就去选择一个合适的单招补习,那么博大单招在这方面的优势到底怎么样?能不能帮助孩子更好地提升呢?今天我们就来一起好好了解一下。 一、博大单招在文化课提升方面优势如何? 博大单招在文化课提升这方面那真的是研究得透透的 -
 “琨玉秋霜”怎么读?到底有什么含义?“琨玉秋霜” 中的“玉” 和 “秋霜” 都是自带高洁感的意象,可 “琨” 字到底读 “kūn” 还是 “hún”?单看字面像在描绘玉石与秋霜的景致,却猜不透为何要将这两种事物组合,更不清楚它的核心指向是写景、咏物还是喻人。今天咱们先把读音校准,再拆解这四字里藏着的纯粹与庄重。 一、“琨玉秋霜”
“琨玉秋霜”怎么读?到底有什么含义?“琨玉秋霜” 中的“玉” 和 “秋霜” 都是自带高洁感的意象,可 “琨” 字到底读 “kūn” 还是 “hún”?单看字面像在描绘玉石与秋霜的景致,却猜不透为何要将这两种事物组合,更不清楚它的核心指向是写景、咏物还是喻人。今天咱们先把读音校准,再拆解这四字里藏着的纯粹与庄重。 一、“琨玉秋霜”
-
 2022高考英语基础知识点!西安伊顿老师带你了解!2022高考英语基础知识点!西安伊顿老师带你了解!高中的英语是一个需要长期积累以及记忆的科目,在高考中只有针对这些知识进行一定的了解和积累,才可以在考试中取得好成绩。针对这种情况,小编请到了西安伊顿老师来给大家总结归纳一下关于高考英语基础知识点的记忆内容,希望对大家有所帮助。对于英语还是需要靠日
2022高考英语基础知识点!西安伊顿老师带你了解!2022高考英语基础知识点!西安伊顿老师带你了解!高中的英语是一个需要长期积累以及记忆的科目,在高考中只有针对这些知识进行一定的了解和积累,才可以在考试中取得好成绩。针对这种情况,小编请到了西安伊顿老师来给大家总结归纳一下关于高考英语基础知识点的记忆内容,希望对大家有所帮助。对于英语还是需要靠日 -
 关于“呐喊与行动那个更重要”的辩论稿写作指导!一直以来,辩论稿的写作都是大家司空见惯的,但是也是很多同学容易忽视的。现在的语文作文考察的范围和广度越来越大,涉及到的文体也越来越多,因此大家在备考语文作文的时候,还是要增加自己的知识面,增加自己的见识。辩论稿大家见得比较多,但是在语言文字上以及结构上的学习,还是非常值得探究的,下面小编给大家分享了一则辩论稿,大家可以练习一下。
关于“呐喊与行动那个更重要”的辩论稿写作指导!一直以来,辩论稿的写作都是大家司空见惯的,但是也是很多同学容易忽视的。现在的语文作文考察的范围和广度越来越大,涉及到的文体也越来越多,因此大家在备考语文作文的时候,还是要增加自己的知识面,增加自己的见识。辩论稿大家见得比较多,但是在语言文字上以及结构上的学习,还是非常值得探究的,下面小编给大家分享了一则辩论稿,大家可以练习一下。 -
 “直播带货”有关的作文写作指导!立意和审题指导!高中的作文写作更多的是来自于社会现象的思考,或者生活的思考,所以高中的同学在写作文的时候可以从生活细节入手,寻找素材,因为任何题目都是取之于生活,进而引发的一系列的思考行为。本次伊顿教育小编给大家分享的这篇作文也是一个社会现象的评述,材料内容是关于“直播带货”,这个大家都是不陌生的,而且有的同学也是参与者,所以对于此也是非常的熟悉的。下面我们可以来看看这篇作文写作的指导。
“直播带货”有关的作文写作指导!立意和审题指导!高中的作文写作更多的是来自于社会现象的思考,或者生活的思考,所以高中的同学在写作文的时候可以从生活细节入手,寻找素材,因为任何题目都是取之于生活,进而引发的一系列的思考行为。本次伊顿教育小编给大家分享的这篇作文也是一个社会现象的评述,材料内容是关于“直播带货”,这个大家都是不陌生的,而且有的同学也是参与者,所以对于此也是非常的熟悉的。下面我们可以来看看这篇作文写作的指导。 -
 2021年9月山水联盟高三开学联考数学试卷及答案(原版)!2021年9月山水联盟高三开学联考已经结束,伊顿教育小编给大家整理了本次联考的数学试卷以及答案,各位相关的小伙伴可以参考一下。对于高三的学习,小编建议大家在每一次的考试之后,都能够仔细的分析一下自己的失分点,对于自己没有掌握的知识点可以尽早的掌握。
2021年9月山水联盟高三开学联考数学试卷及答案(原版)!2021年9月山水联盟高三开学联考已经结束,伊顿教育小编给大家整理了本次联考的数学试卷以及答案,各位相关的小伙伴可以参考一下。对于高三的学习,小编建议大家在每一次的考试之后,都能够仔细的分析一下自己的失分点,对于自己没有掌握的知识点可以尽早的掌握。


















 All right reserved
All right reserved
