高考数学综合大题为什么难得分?大题得高分的诀窍是什么?
尽管距离高考还有一段时间,对于基础较差的同学来说,某些内容可能会显得晦涩难以理解。在高考紧张的氛围下,学生们的注意力会高度集中。这正是充分利用“认知转变”的最佳时机,积极备考的时刻。

在备考过程中,命运总是喜欢青睐那些认真努力、付出卓越努力的学生。如果能够在二轮复习中做得当,即使成绩只提高了十几分,也会轻松把握。
在导数和圆锥曲线部分,我们已经介绍了解决难题的“通法通解”的思路。大家务必在接下来的时间里通过实践、反思和领会,反复地练习和总结。否则,就无法学会如何思考、处理和转化问题。
接下来,我们将讨论立体几何部分的相关高考考点及解题思路。本质上,这意味着将三维立体问题转化为二维平面问题来解答。虽然解三角形的题目可能不再是解答题中的重点,但解三角形的知识会融入到立体几何和圆锥曲线部分,进行联合考察。因此,解三角形类的题目并没有被排除,而是被考察得更加深入和隐蔽了。
解三角形的正、余定理以及三角函数角度之间的和、差、积等变换,在圆锥曲线和立体几何中同样适用。因此,务必特别注意总结新型考题的解法!
立体几何大题所问不外乎:空间位置、空间角度、空间距离、面积体积问题。其中涉及存在性(Ex:考虑位置关系时,方法穷尽用假设),最优问题是其重点和难点,关键在于如何通过做辅助线予以转化!
证明位置关系:优先考虑三垂线定理及其逆定理来证明线线垂直(高频次考点)。该类问题关键在于结合已知条件和性质,通过添加辅助线或面来寻找解题思路。
三垂线定理:平面内的一条直线,如果与穿过这个平面的一条斜线在这个平面上的射影垂直,那么它也和这条斜线垂直。
逆定理则:如果平面内一条直线与该平面的一条斜线垂直,则这条直线也垂直于那条斜线在平面内的射影。
注意:确定哪些直线是外角平分线,哪些直线是与三角形垂直的直线
空间角的计算:解题步骤:一作、二证、三算;若用向量,那就是一证、二算。这类题目关键在于作出垂线并找到射影进行计算。二面角问题是历年高频次考点,一般将空间角转化为平面角来处理,通常根据定义法、三垂线定理及其逆定理法或垂面法来找到平面角。此外也涉及三余弦定理来处理所求问题。
(1)两条异面直线所成的角:①平移法②补形法③向量法(建立坐标系,求两条直线的坐标,)
(2)直线和平面所成的角:①作出直线和平面所成的角,关键是作垂线,找射影转化到同一三角形中计算,或用向量计算。②用公式计算。
(3)二面角:①平面角的作法:(i)定义法;(ii)三垂线定理及其逆定理法;(iii)垂面法。②平面角的计算法:(i)找到平面角,然后在三角形中计算(解三角形)或用向量计算;(ii)射影面积法;(iii)向量夹角公式。
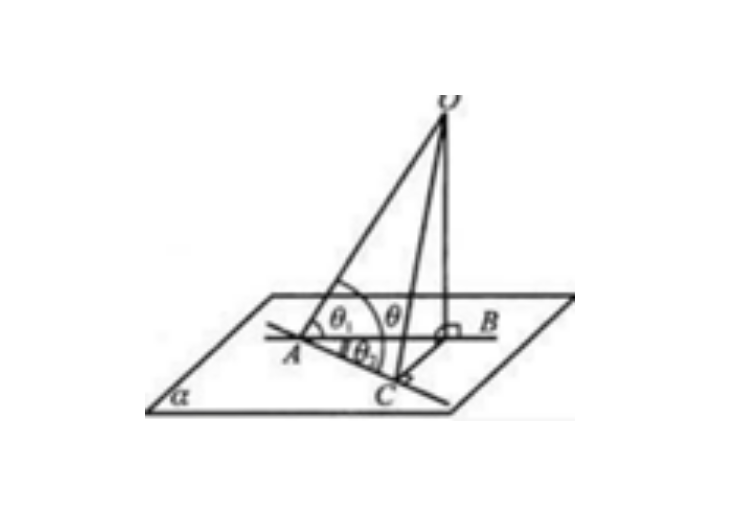
三余弦定理:设A为面上一点,过A的斜线AO在面上的射影为AB,AC为
面上的一条直线,那么∠OAC,∠BAC,∠OAB三角的余弦关系为:cos∠OAC=cos∠BAC×cos∠OAB (∠BAC和∠OAB只能是锐角)
回顾一下,解决立体几何问题也并不复杂。只要掌握方法,问题就会迎刃而解。好了,今天就到这吧。其他类型的立体几何问题,我们下次再分享。同学们记住,“不放弃”是每个高考人必须坚定的信念!不留遗憾到终生。
- 热门课程
- 热门资讯
- 热门资料
- 热门福利
-
 黄河小班课人数多吗?教学效果怎么样?黄河小班课之前就有家长和学生想要了解过,今天为了满足大家的要求,小编就来好好给大家解答一下关于黄河小班课的一些内容,让大家能够更加方便地做出选择。 一、黄河小班课人数多吗? 黄河小班课的人数控制得挺讲究,既不是那种三五个人的微型小组,也不会像其他学校那样挤着四五十个人,一个班大概在6到15人
黄河小班课人数多吗?教学效果怎么样?黄河小班课之前就有家长和学生想要了解过,今天为了满足大家的要求,小编就来好好给大家解答一下关于黄河小班课的一些内容,让大家能够更加方便地做出选择。 一、黄河小班课人数多吗? 黄河小班课的人数控制得挺讲究,既不是那种三五个人的微型小组,也不会像其他学校那样挤着四五十个人,一个班大概在6到15人 -
 “白驹过隙”怎么读?到底有什么含义?“白驹过隙” 是形容时光的经典表达,可你真能笃定 “驹” 字读 “jū” 而非 “jú”?而且 “白驹” 为何是 “白色的小马”,“过隙” 又特指什么缝隙? 一、“白驹过隙”怎么读? “白驹过隙”的正确读音是bái jū guò xì,“白驹”指白色的骏马,常被引申为太阳的光芒或飞速流逝的时
“白驹过隙”怎么读?到底有什么含义?“白驹过隙” 是形容时光的经典表达,可你真能笃定 “驹” 字读 “jū” 而非 “jú”?而且 “白驹” 为何是 “白色的小马”,“过隙” 又特指什么缝隙? 一、“白驹过隙”怎么读? “白驹过隙”的正确读音是bái jū guò xì,“白驹”指白色的骏马,常被引申为太阳的光芒或飞速流逝的时 -
 博大单招在文化课提升方面优势如何?补习效果好吗?单招相信第一次接触的家长和同学们有很多问题都不了解,很多家长为了让孩子更好地学习就去选择一个合适的单招补习,那么博大单招在这方面的优势到底怎么样?能不能帮助孩子更好地提升呢?今天我们就来一起好好了解一下。 一、博大单招在文化课提升方面优势如何? 博大单招在文化课提升这方面那真的是研究得透透的
博大单招在文化课提升方面优势如何?补习效果好吗?单招相信第一次接触的家长和同学们有很多问题都不了解,很多家长为了让孩子更好地学习就去选择一个合适的单招补习,那么博大单招在这方面的优势到底怎么样?能不能帮助孩子更好地提升呢?今天我们就来一起好好了解一下。 一、博大单招在文化课提升方面优势如何? 博大单招在文化课提升这方面那真的是研究得透透的 -
 “琨玉秋霜”怎么读?到底有什么含义?“琨玉秋霜” 中的“玉” 和 “秋霜” 都是自带高洁感的意象,可 “琨” 字到底读 “kūn” 还是 “hún”?单看字面像在描绘玉石与秋霜的景致,却猜不透为何要将这两种事物组合,更不清楚它的核心指向是写景、咏物还是喻人。今天咱们先把读音校准,再拆解这四字里藏着的纯粹与庄重。 一、“琨玉秋霜”
“琨玉秋霜”怎么读?到底有什么含义?“琨玉秋霜” 中的“玉” 和 “秋霜” 都是自带高洁感的意象,可 “琨” 字到底读 “kūn” 还是 “hún”?单看字面像在描绘玉石与秋霜的景致,却猜不透为何要将这两种事物组合,更不清楚它的核心指向是写景、咏物还是喻人。今天咱们先把读音校准,再拆解这四字里藏着的纯粹与庄重。 一、“琨玉秋霜”
-
 2022高考英语基础知识点!西安伊顿老师带你了解!2022高考英语基础知识点!西安伊顿老师带你了解!高中的英语是一个需要长期积累以及记忆的科目,在高考中只有针对这些知识进行一定的了解和积累,才可以在考试中取得好成绩。针对这种情况,小编请到了西安伊顿老师来给大家总结归纳一下关于高考英语基础知识点的记忆内容,希望对大家有所帮助。对于英语还是需要靠日
2022高考英语基础知识点!西安伊顿老师带你了解!2022高考英语基础知识点!西安伊顿老师带你了解!高中的英语是一个需要长期积累以及记忆的科目,在高考中只有针对这些知识进行一定的了解和积累,才可以在考试中取得好成绩。针对这种情况,小编请到了西安伊顿老师来给大家总结归纳一下关于高考英语基础知识点的记忆内容,希望对大家有所帮助。对于英语还是需要靠日 -
 关于“呐喊与行动那个更重要”的辩论稿写作指导!一直以来,辩论稿的写作都是大家司空见惯的,但是也是很多同学容易忽视的。现在的语文作文考察的范围和广度越来越大,涉及到的文体也越来越多,因此大家在备考语文作文的时候,还是要增加自己的知识面,增加自己的见识。辩论稿大家见得比较多,但是在语言文字上以及结构上的学习,还是非常值得探究的,下面小编给大家分享了一则辩论稿,大家可以练习一下。
关于“呐喊与行动那个更重要”的辩论稿写作指导!一直以来,辩论稿的写作都是大家司空见惯的,但是也是很多同学容易忽视的。现在的语文作文考察的范围和广度越来越大,涉及到的文体也越来越多,因此大家在备考语文作文的时候,还是要增加自己的知识面,增加自己的见识。辩论稿大家见得比较多,但是在语言文字上以及结构上的学习,还是非常值得探究的,下面小编给大家分享了一则辩论稿,大家可以练习一下。 -
 “直播带货”有关的作文写作指导!立意和审题指导!高中的作文写作更多的是来自于社会现象的思考,或者生活的思考,所以高中的同学在写作文的时候可以从生活细节入手,寻找素材,因为任何题目都是取之于生活,进而引发的一系列的思考行为。本次伊顿教育小编给大家分享的这篇作文也是一个社会现象的评述,材料内容是关于“直播带货”,这个大家都是不陌生的,而且有的同学也是参与者,所以对于此也是非常的熟悉的。下面我们可以来看看这篇作文写作的指导。
“直播带货”有关的作文写作指导!立意和审题指导!高中的作文写作更多的是来自于社会现象的思考,或者生活的思考,所以高中的同学在写作文的时候可以从生活细节入手,寻找素材,因为任何题目都是取之于生活,进而引发的一系列的思考行为。本次伊顿教育小编给大家分享的这篇作文也是一个社会现象的评述,材料内容是关于“直播带货”,这个大家都是不陌生的,而且有的同学也是参与者,所以对于此也是非常的熟悉的。下面我们可以来看看这篇作文写作的指导。 -
 2021年9月山水联盟高三开学联考数学试卷及答案(原版)!2021年9月山水联盟高三开学联考已经结束,伊顿教育小编给大家整理了本次联考的数学试卷以及答案,各位相关的小伙伴可以参考一下。对于高三的学习,小编建议大家在每一次的考试之后,都能够仔细的分析一下自己的失分点,对于自己没有掌握的知识点可以尽早的掌握。
2021年9月山水联盟高三开学联考数学试卷及答案(原版)!2021年9月山水联盟高三开学联考已经结束,伊顿教育小编给大家整理了本次联考的数学试卷以及答案,各位相关的小伙伴可以参考一下。对于高三的学习,小编建议大家在每一次的考试之后,都能够仔细的分析一下自己的失分点,对于自己没有掌握的知识点可以尽早的掌握。


















 All right reserved
All right reserved
