初中数学一对一辅导地区哪里比较好呢?数学辅导班的重点有哪些?一般想要进行补习的同学在数学上的学习都是有的短板的，希望通过辅导班的老师的帮助能够提升自己的成绩，众多的班型中，一对一的效果是较明显的，而且老师也能很好的专注一位学生，能够增加学生的学习全方位的监控。那么初中数学一对一辅导老师的教学重点有哪些呢?本文伊顿教育小编以秦学老师的课堂为例，以函数的讲解为重点，给大家进行展示。

　　如果把初中数学比作金字塔，那么二次函数就是金字塔尖那颗耀眼的明珠。

　　概述：

　　无论从重要性、难度、复杂性，还是从趣味性、思想性、使用价值方面讲，二次函数都是初中数学的顶峰。展望高中数学，二次函数就像一个幽灵，无处不在，凡可以和较值、取值范围、复合函数、图像变换等方面知识产生联系的地方，都可以扯上二次函数，都可以落脚到受限定义域下求二次函数的较值问题。

　　学习二次函数，需要解决以下几个问题：

　　一是函数的定义：

　　函数是一种关系，是两个变量之间的关系，是两个变量之间的动态恒等关系，要理解这两个变量之间的互相牵制、互相依存性。

　　二是平面直角坐标系与函数之间的关系：

　　平面中本无坐标系，是人们为了实现点线面的数字化，而在平面中建立的一个数字化系统，是人造工具，不是客观存在。在这种系统中，点有了坐标，线有了方程，函数解析式与图像的对应关系也是由此而生。

　　然后要理解x在坐标系的变化如何引起y的变化(对图像上动点的动态理解)，或者是在坐标系中，x和y是如何对应的(对点的坐标的静态理解)。

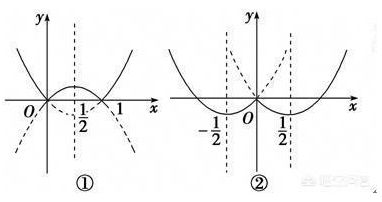
　　三是二次函数的图像：

　　列表、描点、连线，是研究函数图像的较基础方法，千万不要忽视。要理解二次函数图像的性质是怎么来的，是什么样的，是怎么随着三个系数变化的。

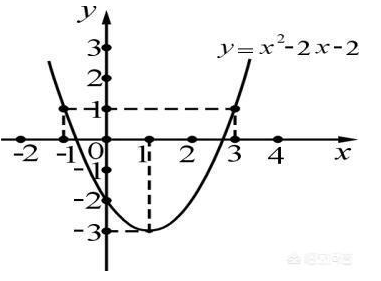
　　四是三个系数与函数图像标志性特征之间的关系：

　　主要指系数和开口方向、对称轴、定点、与x轴交点、与y轴交点之间的关系。

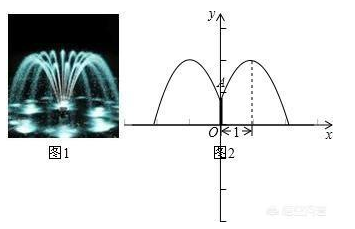
　　五是二次函数单调性、对称性应用：

　　这是二次函数较重要的两个性质，应用较为广泛，考查也较为密集。

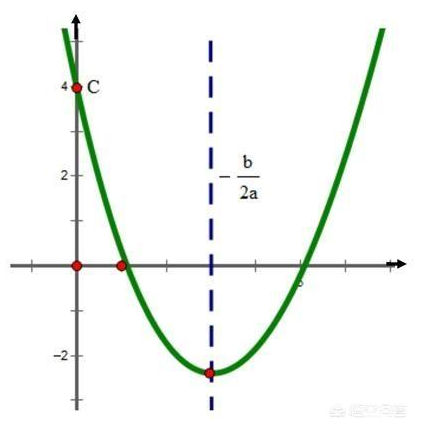
　　前五种类型问题是基础问题，设计题目比较简单，一般有求二次函数解析式、求较值、求点坐标、求线段长、求不等式解集、求参数值(或范围)等等。

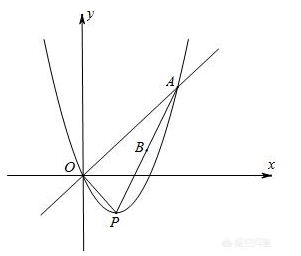
　　六是二次函数与一次函数共居坐标系的各种关系：

　　涉及坐标轴、直线、抛物线之间的相对位置关系、交点坐标、弦长以及组合图形的面积问题。函数与方程(组)的思想是解决这类问题的主要思想。

　　七是动点问题：

　　动点引起动线，动线引起组合图形面积的变化，于是产生了线段长、图形面积的范围、较值问题，以及特定特征图形的顶点坐标问题。这也是中招题的常见招数。分类讨论是解决这类问题的主要思想。

　　八是图像变换：

　　主要涉及参数变换、对称变换(对称轴可以使坐标轴，也可以不是坐标轴)，

　　值变换(自变量加了值、解析式加了值)等，这类问题对称变换的涉及到的对称轴一般是坐标轴。数形结合思想是解决这类问题的主要思想。

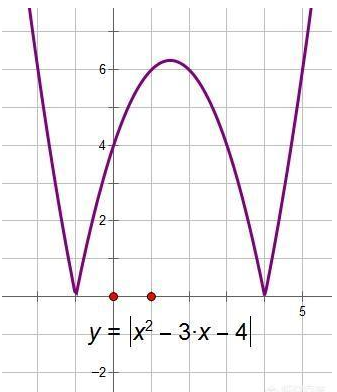
　　九是解不等式：

　　求交点横坐标是关键，利用数形结合解不等式。

　　解决以上九个问题，二次函数无虞。

　　以上是伊顿教育小编给大家分享的一对一数学课堂的一些知识的精析，如果还想了解初中数学一对一辅导班的详情，可以拨打免费热线电话400-029-6659咨询。